9 Optimization in R

Actuaries often write functions (e.g. a likelihood) that have to be optimized. Here you’ll get to know some R functionalities to do optimization.

9.1 Find the root of a function

Consider the function \(f: x \mapsto x^2-3^{-x}\). What is the root of this function over the interval \([0,1]\)?

# in one line of code
uniroot(function(x) x^2-3^(-x), lower=0, upper=1)

$root
[1] 0.68602

$f.root
[1] -8.0827e-06

$iter
[1] 4

$init.it
[1] NA

$estim.prec
[1] 6.1035e-05

? uniroot
# in more lines of code
f <- function(x){
    x^2-3^(-x)
}
# calculate root
opt <- uniroot(f, lower=0, upper=1)
# check arguments
names(opt)

[1] "root"       "f.root"     "iter"       "init.it"    "estim.prec"

# evaluate 'f(.)' in the root
f(opt$root)

[1] -8.0827e-06

# visualize the function
range <- seq(-2, 2, by=0.2)
plot(range, f(range), type="l")
points(opt$root, f(opt$root), pch=20)
segments(opt$root, -7, opt$root, 0, lty=2)
segments(-3, 0, opt$root, 0, lty=2)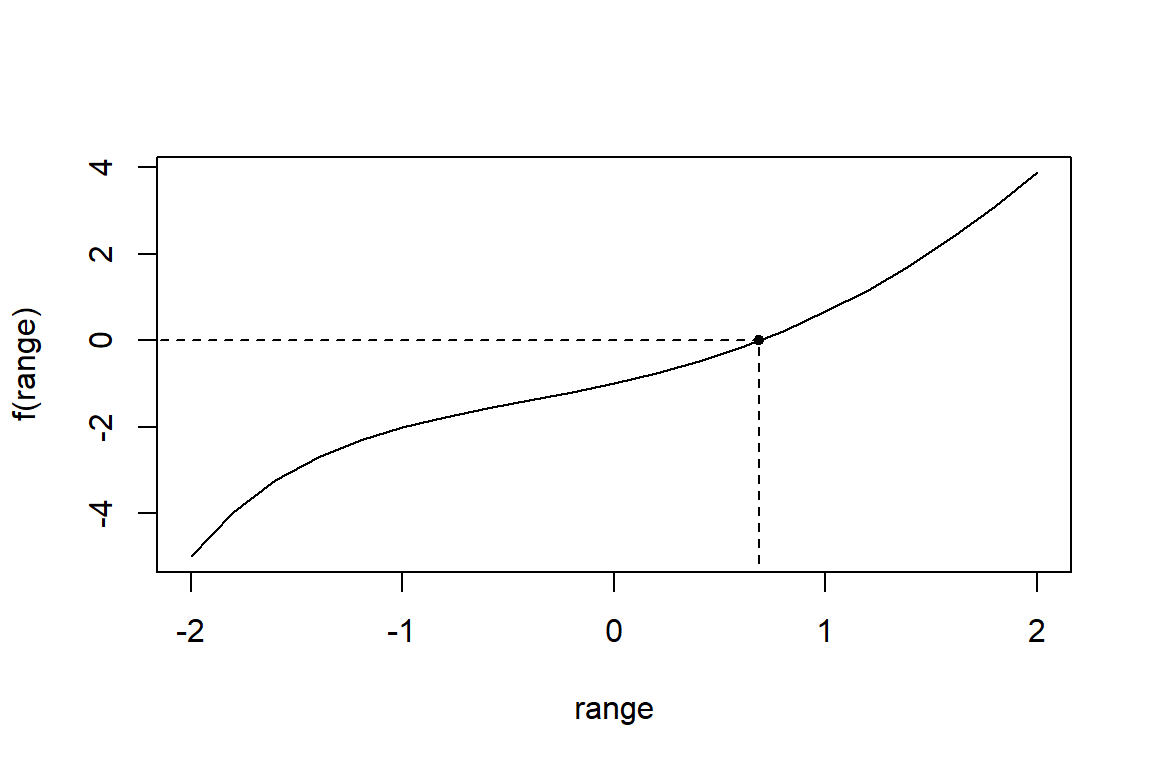

---

9.2 Find the maximum of a function

You look for the maximum of the beta density with a given set of parameters.

# visualize the density
shape1 <- 3
shape2 <- 2
x <- seq(from=0, to=1, by=0.01)
curve(dbeta(x,shape1,shape2), xlim=range(x))

opt_beta <- optimize(dbeta, interval=c(0,1), maximum=TRUE, shape1, shape2)
points(opt_beta$maximum, opt_beta$objective, pch=20, cex=1.5)
segments(opt_beta$maximum, 0, opt_beta$maximum, opt_beta$objective, lty=2)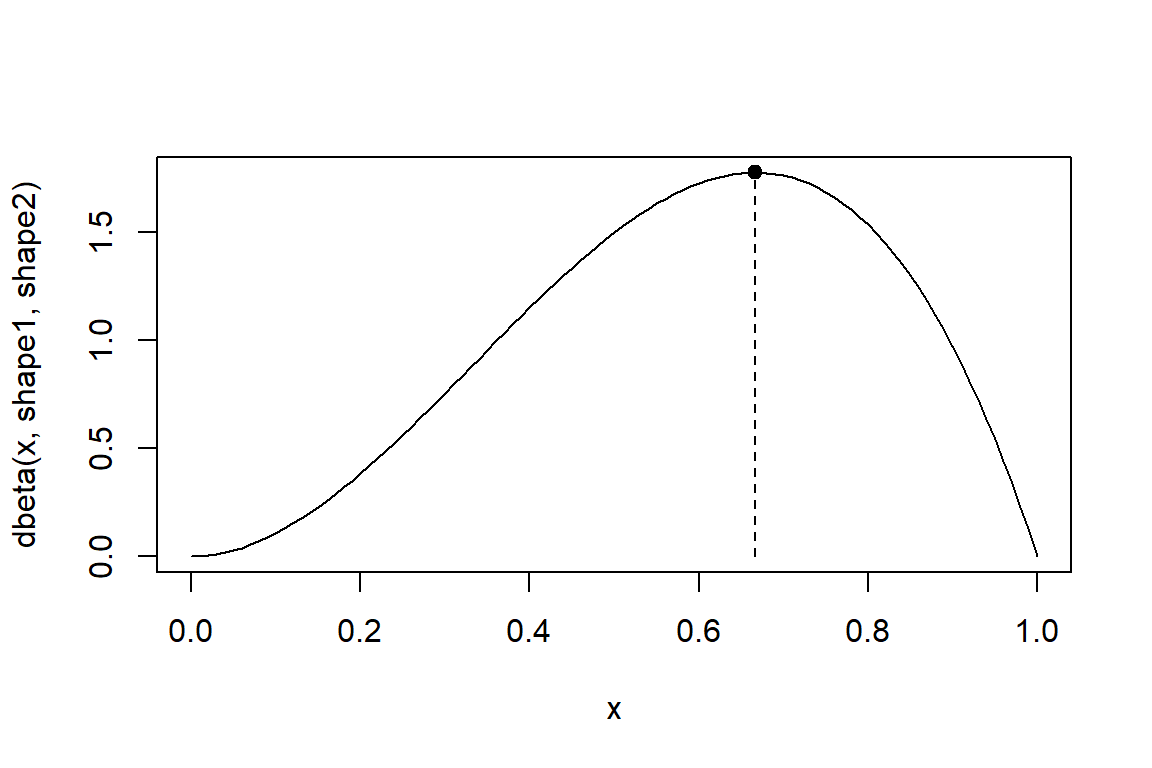

---

9.3 Do Maximum Likelihood Estimation (MLE)

nsim <- 10000
x <- rgamma(nsim, shape=3, rate=1.5)
# calculate log-likelihood
f <- function(p,x){
    -sum(dgamma(x, shape=p[1], rate=p[2], log=TRUE))
}
nlm(f, c(1, 1), x=x)

Warning in dgamma(x, shape = p[1], rate = p[2], log = TRUE): NaNs produced

Warning in nlm(f, c(1, 1), x = x): NA/Inf replaced by maximum positive value

Warning in dgamma(x, shape = p[1], rate = p[2], log = TRUE): NaNs produced

Warning in nlm(f, c(1, 1), x = x): NA/Inf replaced by maximum positive value

Warning in dgamma(x, shape = p[1], rate = p[2], log = TRUE): NaNs produced

Warning in nlm(f, c(1, 1), x = x): NA/Inf replaced by maximum positive value

$minimum
[1] 14407

$estimate
[1] 2.9792 1.4956

$gradient
[1] -0.0024856  0.0026648

$code
[1] 1

$iterations
[1] 14

# same example, now use 'optim'
optim(c(1, 1), f, x=x)

$par
[1] 2.9790 1.4953

$value
[1] 14407

$counts
function gradient 
      67       NA 

$convergence
[1] 0

$message
NULL